Are you having trouble finding 'integration of rational functions by partial fractions homework'? You can find all of the material on this webpage.
Table of contents
- Integration of rational functions by partial fractions homework in 2021
- Integration of rational functions by partial fractions calculator
- Partial fractions worksheet
- Partial fraction examples
- Partial fraction rules
- Integration by partial fractions pdf
- Integration by partial fractions examples and solutions pdf
- Partial fraction integration calculator
Integration of rational functions by partial fractions homework in 2021
 This picture shows integration of rational functions by partial fractions homework.
This picture shows integration of rational functions by partial fractions homework.
Integration of rational functions by partial fractions calculator
 This picture demonstrates Integration of rational functions by partial fractions calculator.
This picture demonstrates Integration of rational functions by partial fractions calculator.
Partial fractions worksheet
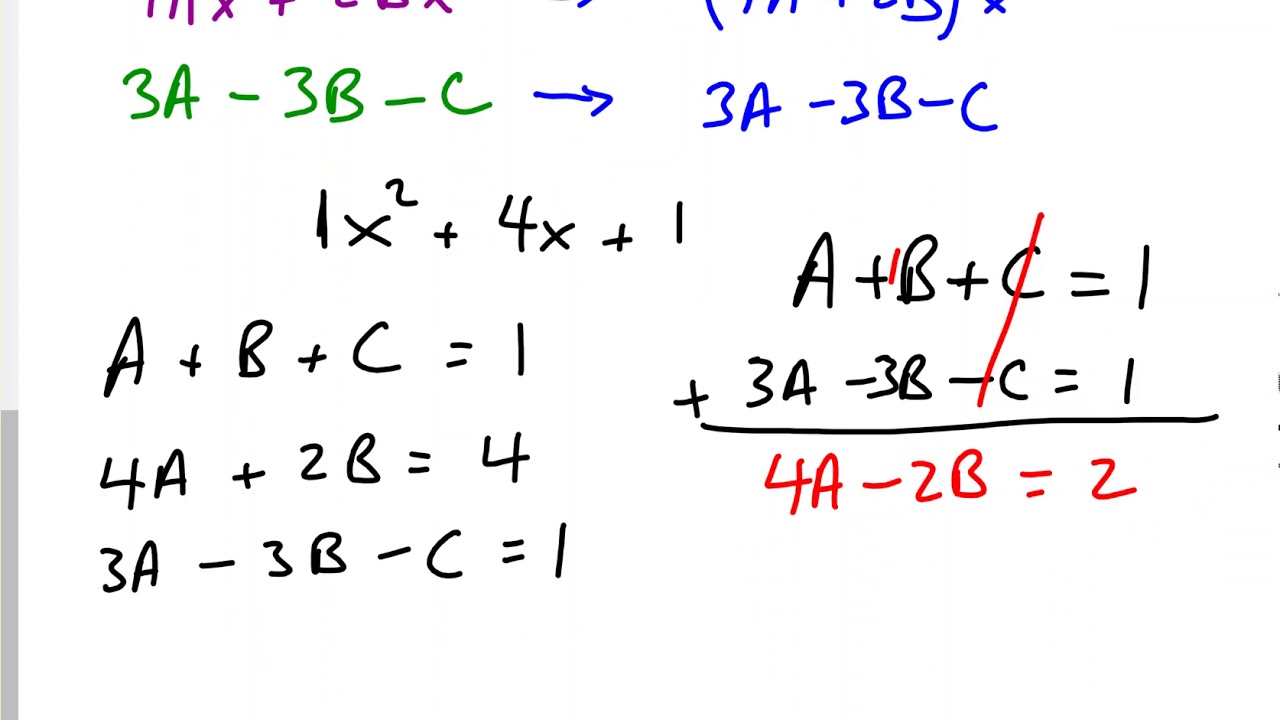 This picture demonstrates Partial fractions worksheet.
This picture demonstrates Partial fractions worksheet.
Partial fraction examples
 This image shows Partial fraction examples.
This image shows Partial fraction examples.
Partial fraction rules
 This picture demonstrates Partial fraction rules.
This picture demonstrates Partial fraction rules.
Integration by partial fractions pdf
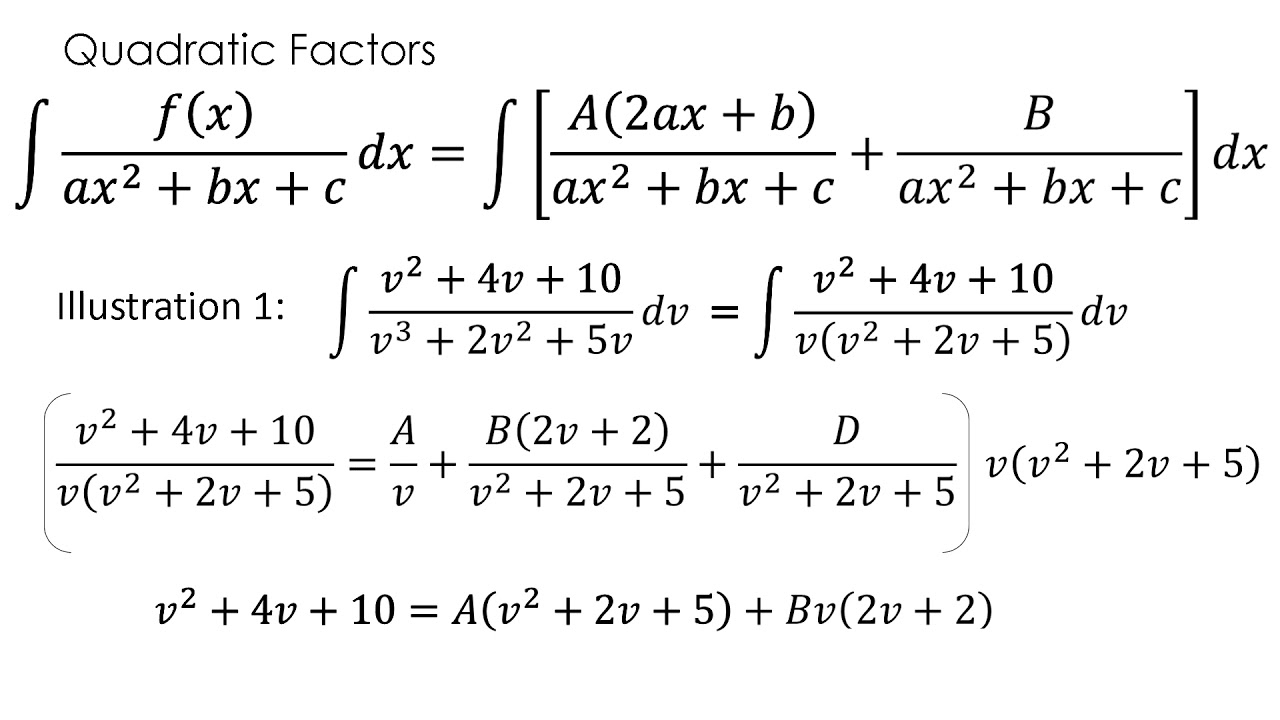 This picture representes Integration by partial fractions pdf.
This picture representes Integration by partial fractions pdf.
Integration by partial fractions examples and solutions pdf
 This picture shows Integration by partial fractions examples and solutions pdf.
This picture shows Integration by partial fractions examples and solutions pdf.
Partial fraction integration calculator
 This picture illustrates Partial fraction integration calculator.
This picture illustrates Partial fraction integration calculator.
How to get the general form of the partial fraction decomposition?
Once we’ve done this we can do all the integrals in the problem. The first two use the substitution u = x − 4 u = x − 4, the third uses the substitution v = x 2 + 3 v = x 2 + 3 and the fourth term uses the formula given above for inverse tangents. Let’s first get the general form of the partial fraction decomposition.
When do partial fractions have to be factored?
Recall that the degree of a polynomial is the largest exponent in the polynomial. Partial fractions can only be done if the degree of the numerator is strictly less than the degree of the denominator. That is important to remember. So, once we’ve determined that partial fractions can be done we factor the denominator as completely as possible.
How are partial fractions used to integrate rational functions?
7.4 Integration by Partial Fractions The method of partial fractions is used to integrate rational functions. That is, we want to compute Z P(x) Q(x) dx where P, Q are polynomials.
Last Update: Oct 2021